La vérité
Introduction.
Socrate (V Siècle av JC) : « je
sais une chose c’est que je ne sais rien ». Etre conscient de son ignorance est la première condition pour
rechercher la vérité.
I / Vérité et
opinion
1 / Qu’est-ce que l’opinion?
L'opinion se définit essentiellement par le rapport que le sujet entretient avec
ce qu'il affirme. Tous les caractères mis en évidence qualifient en effet le
rapport que le sujet entretient avec son opinion : immédiateté, irréflexion,
passivité, utilité. Rien ici qui soit relatif au contenu des opinions.
2 / Peut-on rompre avec nos opinions ?
a-2-1 La
rencontre avec l'altérité
Echec :
Le rejet de l'altérité (Socrate accusé
d’impiété envers les dieux et de corruption de la jeunesse. Il est condamné à
mort le par tribunal d’Athènes, par absorption de la ciguë)
a-2-2 Le désir, le souci de la vérité, notion
d’idéologie
Echec :
Le Relativisme
« L’homme
est la mesure de toute chose » Protagoras..
L’allégorie de la caverne – Platon. La République.
Livre VII. Vidéos
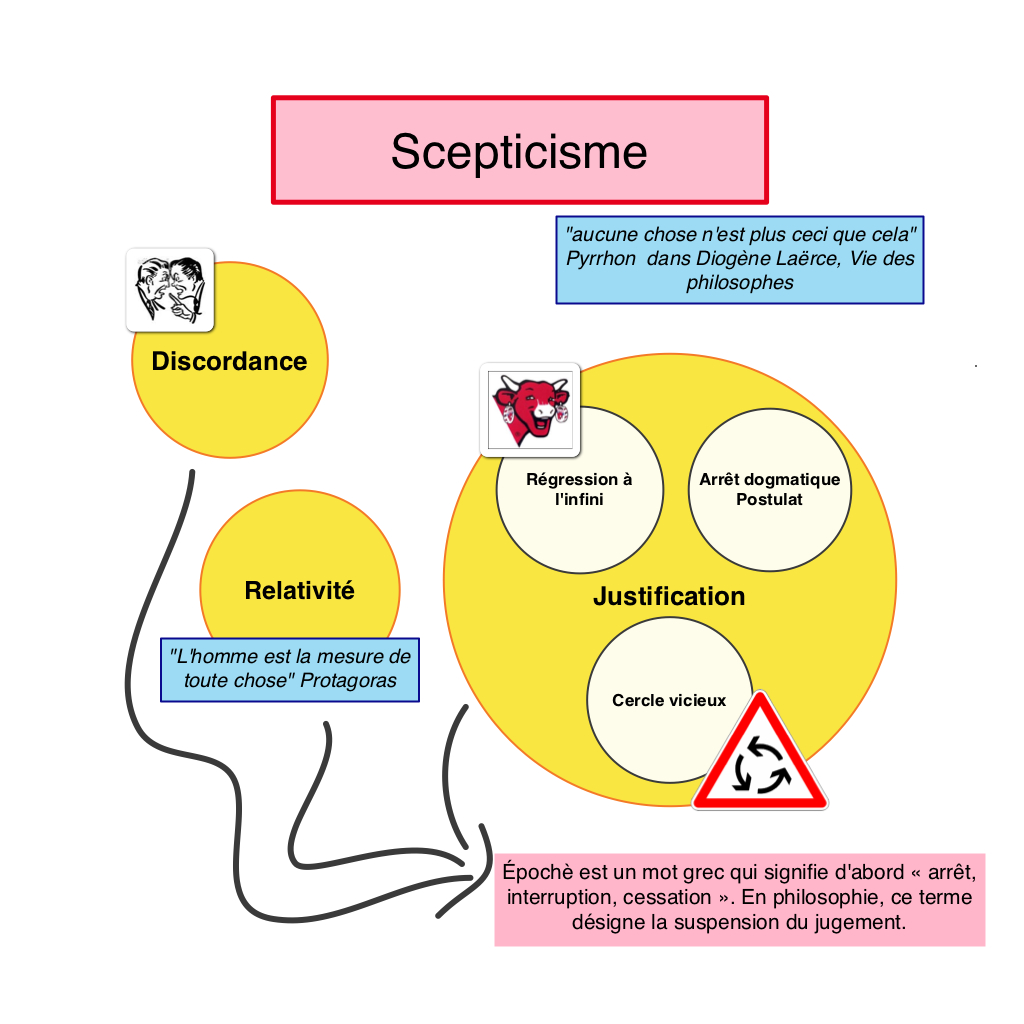
3 / Le
scepticisme
Les sceptiques Antiques (fondateur Pyrrhon d’Élis env.340-275 av. JC) ont
concoctés diverses techniques argumentatives, qui sont autant de médicaments
destinés à combattre les ravages du dogmatisme.
« Tous les abus du
monde s’engendrent de ce qu’on nous apprend craindre de faire profession de
notre ignorance. » Montaigne
Les différents arguments des sceptiques (les 5 modes d’Agrippa) Critique :
Théorie contradictoire en théorie et impossible dans la pratique
III /
Critères de la vérité
1 / Évidence, critère de vérité du
jugement
« La vérité est à
elle-même son propre signe » Spinoza. Qui a une vérité, sait en même temps qu’il a une idée vraie.
2 / La vérité, est-ce la copie de la
réalité
La
vérité, c’est la conformité de notre pensée aux choses.
On
définit la vérité comme « adéquation de l’idée à la chose ».La vérité
définit une relation de représentation adéquate. Cependant, pour savoir qu’une
représentation est vraie, il faudrait connaître l’objet en dehors de notre
représentation, or on ne peut le connaître qu’à partir de l’idée que l’on en
possède : notre représentation
3 / La vérité, c’est la
non-contradiction d’un système de jugements
3.1
La vérité formelle : respect des règles logiques
3.2
La vérité expérimentale
Lorsqu’une
théorie falsifiable n’est pas réfutée, nous pouvons considérer qu’elle est
corroborée par l’expérience, mais pas plus ; de cette corroboration,
toujours provisoire, nous pouvons tirer une préférence pour cette théorie, mais
non une certitude. Rationalisme critique de Karl Popper.
Conclusion : Le doute,
c’est le sel de l’esprit, disait Alain. Ni trop, ni pas assez. Attention, à ne pas
se laisser enfermer dans le doute (abdication devant la vérité)
III Vérités scientifiques
1. Schéma d’évolution des sciences- Progrès des sciences
Moteur
du progrès : le fait problème - Evolution des sciences : données socio-historiques
2. Sciences et techniques
-----------------------------------------------------------------------------------------------------------
La Démonstration
Introduction : Déf. : Opération par laquelle une proposition est établie de
manière certaine à partir d’une autre. Prémisses → Conclusion. Le Pb qui guette
la dém n’est autre que le régression à l’infini:n’est-on pas obliger de tj
poser un indémontrable en amont de la dém.
I / Les formes du raisonnement et leurs limites
1 /
La déduction
La déduction est a priori, c’est à dire indépendante de
l’expérience. Une fois établi la vérité des prémisses, on passe de manière nécessaire à la conclusion. Conclure autrement
serait se contredire. Règles logiques. Notion de tautologie. Il faut distinguer dans le raisonnement
la forme du contenu, la vérité formelle ou validité, de la vérité matérielle.
Notion de paralogisme : démonstration fallacieuse, apparence de rigueur.
Notion de sophisme
2 /
Analogie N’est pas un raisonnement logique
valide, simple association mentale. N’aboutit qu’à du probable. (Ex :
analogie pour autrui) Pouvoir de l’analogie, Cf. sciences humaines
3 /
Induction
Ă partir de
l’observation d’un grand nombre de faits (dans des circonstances variées), on
peut par induction, énoncer une loi générale. L’induction est amplifiante. Il
s’agit d’anticiper l’expérience future , c'est-à-dire conclure d’un fait
observé à un autre fait attendu, en nous fondant sur la supposition générale
que l’ordre de la nature est immuable ou que les mêmes causes produisent les
mêmes effets. Le raisonnement inductif est à la base des sciences
expérimentales. Impossible de démontrer les faits. Texte de Hume et Texte de Russell .
La dinde inductiviste de Bertrand Russel :
L’induction est un
raisonnement non fondé logiquement
Rqu : Argumentation
Certes un argument pour être valable exige le respect des
règles de la logique. L’argumentation ouvre à la rationalité d’autres domaines,
inaccessibles à la vérité : décisions morales, politiques,
religieuses. Ce n’est pas parce qu’il
n’est impossible de démontrer la justesse d’une décision morale qu’il est impossible d’argumenter pour
la justifier. Impossibilité de démontrer l’existence de dieu mais possibilité
d’argumenter.
4 Sophismes Powerpoint
Sophismes déductifs, …
II / Tout
démontrer ? Le problème du
fondement
Rqu :Les définitions mathématiques
La définition mathématique est créatrice pas descriptive
( ≠ définition empirique)
Le point mathématique n’existe pas dans la nature, le
mathématicien ne le découvre pas comme le naturaliste découvre un oiseau et en
fait la description. La définition de l’objet mathématique crée l’objet.
1/ Les postulats
Proposition première que le mathématicien demande qu’on
accorde et que l’on a regardé pendant très longtemps comme des vérités
absolues. On peut en réalité construire un système hypothético-déductif tout à
fait cohérent sur d’autres postulats. Relativisation de la vérité des
théorèmes : leurs vérités n’est plus que l’intégration valide au système.
La géométrie d’Euclide est une parmi d’autres.
Cf. Géométries non-euclidiennes Comparaison aux systèmes
métriques par Henri Poincaré.
2/
Dissertation Peut-on tout démontrer ?
Conclusion : Il ne suffit pas de connaître
les lois de la déduction pour atteindre la vérité : la logique (la
non-contradiction) est une condition nécessaire mais non suffisante. Il faut
également s’assurer de la justesse du point de départ. La connaissance n’est
pas seulement faite de déductions, mais également de connaissances simples et
immédiates (intuitions)